Subject Code & Title :- ECON6321 Mineral Economics
Assignment Type :- Mineral Economics
Instructions :-
i. This assignment accounts for __% of the total marks.
ii. Answers should be clear, concise and legible.
iii. The purpose of this assignment is to encourage students to work together and read to answer the questions. Please work together and submit your answers in groups of up to 6 students. Make sure that every member takes part in the group work.
iv. The due date is 20 February 2022
ECON6321 Mineral Economics Assignment
1.Discuss the advantages and disadvantages of the three main types of fiscal regimes
2.Explain resource curse and how it occurs.
3.Given the following optimal control problem.
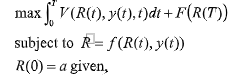
Where R(t) = state variable, y(t) = control variable, t 0 < t < T
Assume no constraints on the control variable
ECON6321 Mineral Economics Assignment
a. Define the Hamiltonian expression for this problem.
b. Derive the necessary conditions for maximisation (taking into account the initial condition.
c. What is the maximum condition?
d. Suppose now that our problem is of free terminal time. What is the free terminal time condition (transversality condition) needed in addition to the conditions derived in part (b)?
e. Write the maximum principle conditions for the problem for the free-terminal time
problem?
4.Given the following continuous time optimal control problem with discounting
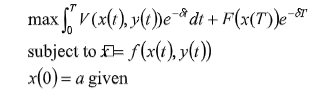
ECON6321 Mineral Economics Assignment
where x(t) = state variable, y(t) = control variable
a. Define the current value Hamiltonian expression for this problem.
b. What are the necessary conditions for the current value Hamiltonian?
c. Define the Hamiltonian expression for this problem.
d. What is (e t ) in the above problem?
ECON6321 Mineral Economics Assignment
5.Suppose the inverse demand function for an exhaustible resource is given by P(t) = q(t) -0.5
Where P(t) is market price and q(t) is harvest rate.
Assuming instantaneous discount rate, , and initial stock R(0) = 1, and no extraction cost,
a. Set up the continuous time, fixed horizon maximization problem for this resource.
b. Derive the current value Hamiltonian.
ORDER This ECON6321 Mineral Economics Assignment NOW And Get Instant Discount
